数学Ⅰ「二次関数」で絶対に抑えておくべきポイント3選

高校1年生で習う「二次関数」の分野は、高校数学の「関数」の考え方に触れる、とても重要な単元です。内容が盛りだくさんの上、演習量を積まなければいけない単元なので、放っておいたら苦手分野になりかねません。今回は、二次関数の分野で特に重要だと思われるポイントを、3つに絞って紹介していきます。

グラフの書き方や関数の概念は、ほかの関数を学ぶ際に必要になる

まず紹介するのは、グラフの書き方、見方についてです。次の式を見てみてください。

この式で表される二次関数のグラフをかきたい、となったとき、まず何をしようと思いますか。

 

そう、平方完成です。

 

では、この平方完成をする理由とは、いったい何でしょうか。

それは、頂点の座標を明らかにして、グラフを描く手掛かりにするため、です。

このように、グラフを描いたりするときに行う操作に対して、その理由をはっきりと理解しておくことは、これから他の関数についてグラフを描いたり、その特徴をつかむときに非常に重要です。

是非、その操作の意味を理解したうえで、問題演習に取り組みましょう。

最大最小問題における場合分けは、論理的な思考のトレーニングになる

 

最大最小問題は、二次関数の中でもかなりの重要度を占める問題です。最大最小問題にもたくさんのバリエーションがありますが、今夏はその中でも「場合分け」が絡んでくる問題を紹介していきます。
次の問題を見てください。

 

 

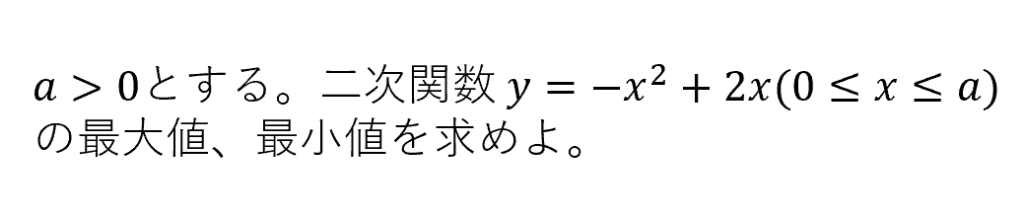
この問題の重要なポイントはどこでしょうか、そう、場合分けです。最大値、最小値は軸の位置や範囲によって変わってくるので、aの値によって場合分けをしなければいけません。

 

 

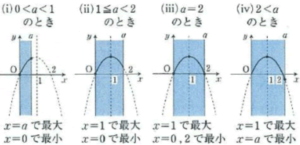
このような場合分けの技術は、ほかの問題でも、論理的に問題を分析するときに必要になってくる力です。これもポイントを押さえたうえで、繰り返し問題に取り組み、自分のものにしましょう。

 

最大最小問題は、入試問題で隠れて出題されることが多い！

上で紹介した最大・最小問題ですが、この問題はほかの分野の問題でもよく出てきます。例えば、三角関数と呼ばれる関数を習うと、

 

 

 

 

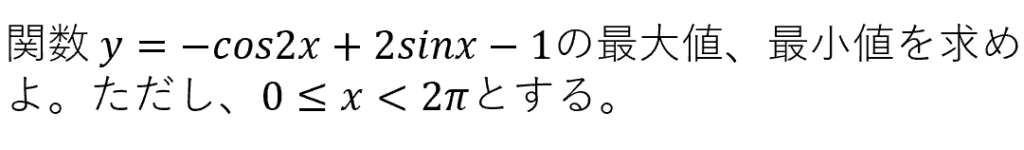
というような問題が出てきます。これは文字の置き換えなどをうまくしたら、二次関数の最大・最小問題に帰着することが出来るのです。この問題のほかにも、図形の面積の最大・最小を考えたりするときなどにも、自分で二次関数を立式して、最大値や最小値を求めよ、という問題は入試問題にも頻出しています。ぜひ、道具として使えるようになるまで、最大・最小問題の演習に取り組んでみてください。

 

まとめ

今回は、二次関数の単元の中で、特に重要なポイントを3つ紹介しました。紹介したグラフの書き方、場合分け、最大最小の応用問題、の3つのポイントは、特に苦手とする生徒が多く、演習を多くこなさないといけないので、肝に銘じて、これからの数学の勉強を頑張ってください！